Recursion

search ood number in list

recurion construction

• end condition
• logic code and recursive call

e.g.

(defun anyoddp (x)
(cond ((null x) nil)
((oddp (first x)) t)
(t (anyoddp (rest x)))))

THE THREE RULES OF RECURSION

1. Know when to stop.
2. Decide how to take one step.
3. Break the journey down into that step plus a smaller journey.

templates

Double-Test Tail Recursion

(DEFUN func (X)
(COND (end-test-1 end-value-1)
(end-test-2 end-value-2)
(T (func reduced-x))))

Single-Test Tail Recursion

(DEFUN func (X)
(COND (end-test end-value)
(T (func reduced-x))))

Augmenting Recursion

Instead of dividing the problem into an initial step plus asmaller journey, they divide it into a smaller journey plus a final step

(DEFUN func (X)
(COND (end-test end-value)
(T (aug-fun aug-val
(func reduced-x)))))

e.g.

(defun count-slices (x)
(cond ((null x) 0)
(t (+ 1 (count-slices (rest x))))))

List-Consing Recursion

As each recursive call returns, we createone new cons cell.

(DEFUN func (N)
(COND (end-test NIL)
(T (CONS new-element
(func reduced-n)))))

Multiple Recursion

(DEFUN func (N)
(COND (end-test-1 end-value-1)
(end-test-2 end-value-2)
(T (combiner (func first-reduced-n)
(func second-reduced-n)))))

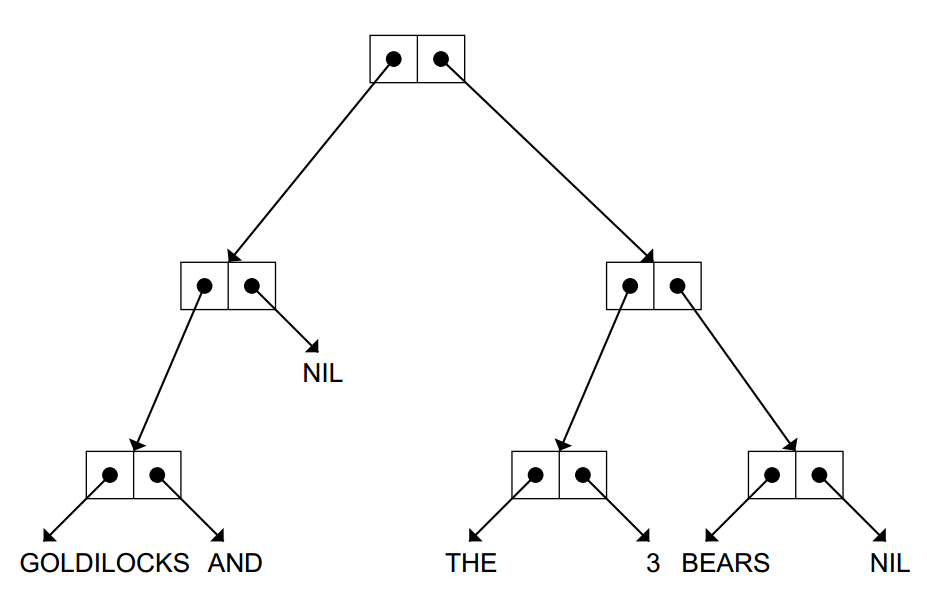
TREES AND CAR/CDR RECURSION

(DEFUN func (X)
(COND (end-test-1 end-value-1)
(end-test-2 end-value-2)
(T (combiner (func (CAR X))
(func (CDR X))))))

THE LABELS SPECIAL FUNCTION

(LABELS ((fn-1 args-1 body-1)
...
(fn-n args-2 body-2))
body)

RECURSIVE DATA STRUCTURES

S-expression (‘‘symbolic expression’’)

defined recursivly

An S-expression is either an atom, ora cons cell whose CAR and CDR parts are S-expressions.

e.g.

tree